On November 6, 2023 (which happens to be my daughter’s birthday), OpenAI released the Assistants API. It empowered developers to integrate AI agents seamlessly into their applications. The OpenAI definition of an assistant is: “An assistant is a purpose-built AI that has specific instructions, leverages extra knowledge, and can call models and tools to perform tasks”. With a little bit of Python coding, and some motivation anyone can create custom application-specific AI assistants.
In this post, we will create an AI assistant that simulates MRI pulse sequences using the Bloch equations. We will explore OpenAI Assistant API’s function calling and knowledge retrieval capabilities. For educational purposes, we will simulate one TR of a spin echo sequence. The simulation will use Bloch equation based RF rotation and T1, T2 relaxation matrices.
But before we get started, let’s familiarize with a few terms. An MRI ‘pulse sequence’ is a series of radiofrequency (RF) pulses and magnetic gradient field waveforms that are played in a specific order to generate, spatially encode and receive tissue-dependent signal. This signal is processed by a computer program to reconstruct the anatomical images. The ‘spin echo sequence‘ is one of the earliest pulse sequences, introduced by Erwin L Hahn in 1950. A spin echo sequence consists of a 90 degree excitation pulse, followed by a wait time t and then a 180 degree refocusing pulse. The signal peak (echo) occurs at time t after the refocusing pulse. The spin echo sequence is highly robust to off-resonance effects but it is generally slow. In clinical use, the spin echo sequence has been replaced by its faster variants like the turbo spin echo. However, due to its immunity to many common MRI artifacts, the spin echo sequence is a great starting point for many MRI research experiments.
Bloch Equations
In 1912, Felix Bloch discovered Nuclear Magnetic Resonance (NMR) which he called nuclear induction in his homonymous paper published in 1946. For this discovery, Felix Bloch and Edward M. Purcell were awarded the Nobel prize for Physics in 1952. NMR is the basis for Magnetic Resonance Imaging (MRI) for which Paul C. Lauterbur and Sir Peter Mansfield were awarded the Nobel prize in Physiology or Medicine in 2003.
The Bloch equations are a set of differential equations that describe the temporal evolution of net magnetization under the effect of external magnetic fields used in an NMR experiment. The Bloch equations can be used to simulate an MRI pulse sequence by solving for the net magnetization under the effect of the RF pulses and gradient waveforms played in the pulse sequence. Rewriting eq (38) from Bloch’s paper
\tag{38a} \dot{M}_x - \gamma(M_y H_z - M_z H_y) + \frac{1}{T_2}M_x = 0\tag{38b}\dot{M}_y - \gamma(M_z H_x - M_x H_z) + \frac{1}{T_2}M_y = 0\tag{38c}\dot{M}_z - \gamma(M_x H_y - M_y H_x) + \frac{1}{T_1}M_z = \frac{1}{T_1}M_0where, in the presence of a static magnetic field B0 and RF field B1, the components of the external magnetic field H are given
H_x=B_1cos(\omega t), H_y=B_1sin(\omega t), H_z=B_0.
In matrix-vector form, the Bloch equation can be represented as
\begin{equation}
\dfrac{dM}{dt} = \begin{bmatrix}
-1/T_2 & \gamma H_z & -\gamma H_y \\
-\gamma H_z & -1/T_2 & \gamma H_x \\
\gamma H_y & -\gamma H_x & -1/T_1 \\
\end{bmatrix} M
+ \begin{bmatrix}
0 \\ 0 \\ M_0/T_1
\end{bmatrix}
\end{equation}The solution to this differential equation (1) is given by
\begin{equation}
M_t = \begin{bmatrix}
e^{-t/T_2} & 0 & 0 \\
0 & e^{-t/T_2} & 0 \\
0 & 0 & e^{-t/T_1} \\
\end{bmatrix} M
+ \begin{bmatrix}
0 \\
0 \\
M_0(1-e^{-t/T1}) \\
\end{bmatrix}
\end{equation}With further derivation, the rotation produced by an RF pulse with flip angle alpha and phase phi can be shown to be
\begin{equation}
R = \begin{bmatrix}
cos^2\phi + sin^2\phi cos\alpha & cos\phi sin\phi(1-cos\alpha) & -sin\phi sin \alpha \\
cos\phi sin\phi(1-cos\alpha) & sin^2\phi+cos^2\phi cos\alpha & cos\phi sin\alpha \\
sin\phi sin\alpha & -sin\alpha cos\phi & cos\alpha \\
\end{bmatrix}
\end{equation}We will implement equations (2) and (3) as Python functions. Our OpenAI assistant will have access to these functions to simulate a spin echo sequence.
OpenAI Pulse Sequence Assistant

Now we will program the Bloch equations and create an OpenAI assistant to simulate a spin echo sequence.
- First we will write a function that implements the relaxation matrix shown in equation (2). The relaxmtx() function takes five inputs, M0 is the initial longitudinal magnetization value, T1 is the tissue-specific T1 relaxation time in seconds, T2 is the tissue-specific T2 relaxation time in seconds, t1t is the time for T1 recovery and t2t is the time for T2 decay. simrelax() is a wrapper function that we will later provide to our OpenAI Assistant.
def relaxmtx(M0, T1, T2, t1t, t2t):
e1 = math.exp(-t1t/T1)
e2 = math.exp(-t2t/T2)
A = np.matrix([[e2, 0, 0],[0, e2, 0],[0, 0, e1]])
B = np.matrix([[0], [0], [M0*(1-e1)]])
return A, B
def simrelax(M0, M, T1, T2, t1t, t2t):
A, B = relaxmtx(M0, T1, T2, t1t, t2t)
return A * np.reshape(M, (3,1)) + B- Similarly, we will write a function that implements the RF rotation matrix show in equation (3). The rfmtx() takes two inputs, alpha is the flip angle in radian units, and phi is the RF phase in radian units. simrf() is a wrapper function that we will provide to our OpenAI Assistant.
def rfmtx(alpha, phi):
R = np.matrix([[math.cos(phi)**2 + math.sin(phi)**2*math.cos(alpha), math.cos(phi)*math.sin(phi)*(1-math.cos(alpha)), -math.sin(phi)*math.sin(alpha)],[math.cos(phi)*math.sin(phi)*(1-math.cos(alpha)), math.sin(phi)**2 + math.cos(phi)**2*math.cos(alpha), math.cos(phi)*math.sin(alpha)],
[math.sin(phi)*math.sin(alpha), -math.sin(alpha)*math.cos(phi), math.cos(alpha)]])
return R
def simrf(M, alpha, phi):
return rfmtx(alpha, phi) * np.reshape(M, (3,1))- It’s time to create our AI assistant! The assistant requires a name, instructions for what the assistant is supposed to do and the model used. We will use the GPT-4 Turbo model that OpenAI announced on DevDay (Nov 6, 2023).
import helper
from openai import OpenAI
client = OpenAI()
assistant = client.beta.assistants.create(
name="Bloch Equation Simulator",
instructions="You are an MR Bloch equation simulator. Simulate pulse sequences using the Bloch equation.",
model="gpt-4-1106-preview",
)
helper.show_json(assistant)Function Calling
From OpenAI “Function calling allows you to describe functions to the Assistants and have it intelligently return the functions that need to be called along with their arguments. The Assistants API will pause execution during a Run when it invokes functions, and you can supply the results of the function call back to continue the Run execution.” We will see an example of how to implement function calling in our assistant.

- First we need to define JSON interfaces to the functions we want the assistant to call. We will define the simrelax() and simrf() interfaces.
- The natural language description of the functions and their parameters are critical. The assistant has access to only these descriptions about our functions. The assistant will use these descriptions to decide which function to call during a conversation. In the function description we clearly describe what the function does and its return values. In the parameter descriptions, we distinctly define the parameters along with their units. Care should be taken to leave no ambiguity in these descriptions.
simrelax_json = {
"name": "simrelax",
"description": "Function to simulate the effect of T1 and T2 relaxation on the magnetization vector. Returns the magnetization vector after the relaxation period.",
"parameters": {
"type": "object",
"properties": {
"M0": {"type": "integer", "description": "scalar value of initial longitudinal magnetization"},
"M": {
"type": "array",
"items": {"type":"number"},
"description": """magnetization vector at the start of the relaxation period"""
},
"T1": {"type": "integer", "description": "T1 relaxation time in seconds units"},
"T2": {"type": "integer", "description": "T2 relaxation time in seconds units"},
"t1t": {"type": "integer", "description": "time for T1 recovery in seconds units"},
"t2t": {"type": "integer", "description": "time for T2 recovery in seconds units"},
},
"required": ["M0","M","T1","T2","t1t","t2t"],
},
}
simrf_json = {
"name": "simrf",
"description": "Function to simulate the effect of an RF pulse on the magnetization vector. Returns the magnetization vector after the RF pulse.",
"parameters": {
"type": "object",
"properties": {
"M": {
"type": "array",
"items": {"type":"number"},
"description": """magnetization vector before the application of the RF pulse"""
},
"alpha": {"type": "integer", "description": "flip angle in radian units"},
"phi": {"type": "integer", "description": "RF pulse phase in radian units"},
},
"required": ["M","alpha","phi"],
},
}- Now we can update the assistant with the new functions. The OpenAI assistant only has access to the JSON interface we provided. The assistant does not know about the implementation details of the functions. This is a crucial point. Your personal code remains secure and inaccessible to the Assistants API!
assistant = client.beta.assistants.update(
assistant.id,
tools=[
{"type":"retrieval"},
{"type":"function", "function":simrf_json},
{"type":"function", "function":simrelax_json},
],
)- You can always see the current status of your assistant in your OpenAI account. Here you can see the assistants name, instructions, model and the functions it has access to. For privacy, I have whited out my assistant key.
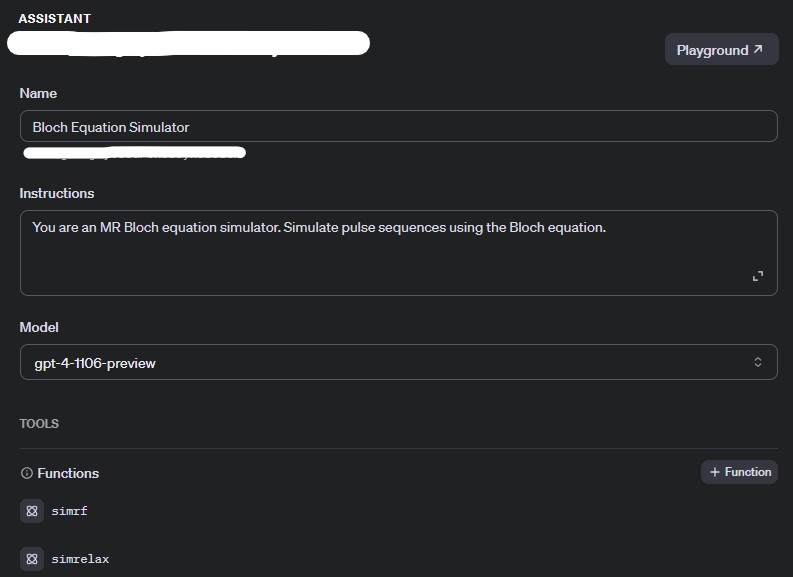
- Let’s talk to our assistant and do our first simulation!
- But before that, we need to know about some Assistants API primitives, namely Threads and Runs. Threads define a scope/state for a conversation with the assistant. Threads encapsulate Runs. Runs execute the assistant on a thread. Following figure from OpenAI illustrates the relation between an Assistant, Thread, and a Run.
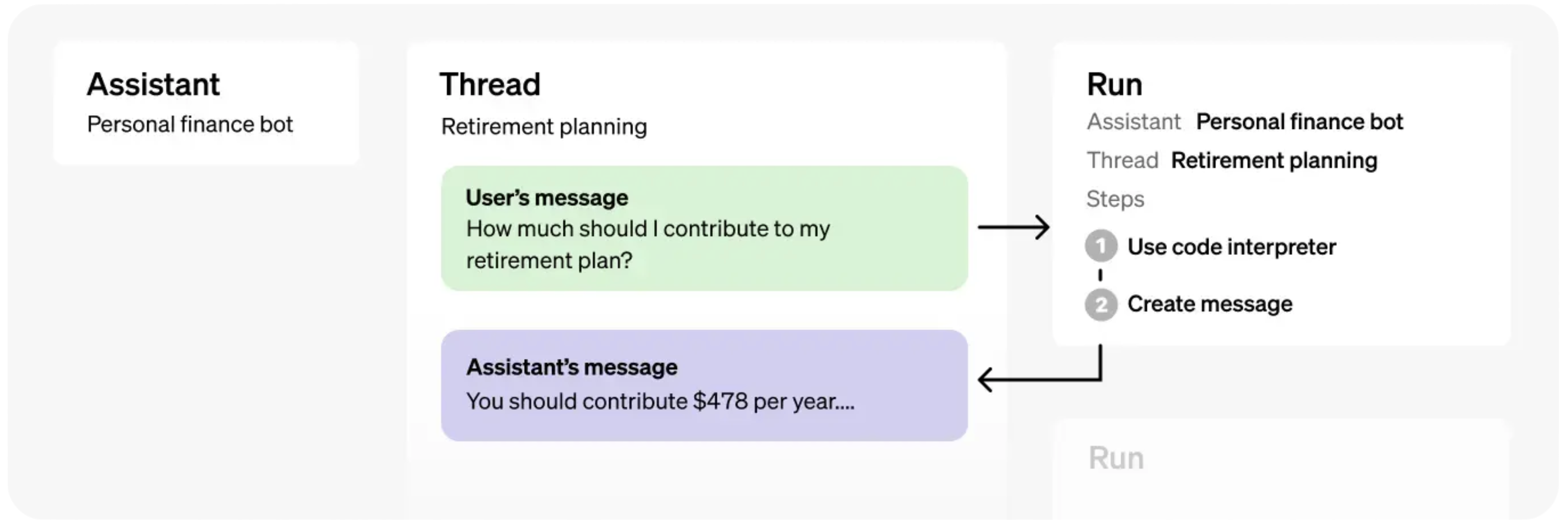
- I have a helper module to create a thread, add messages to it and call run. For brevity, we will not go over the implementation details of the helper module but we will just call it as shown in the next code snippet.
- We will request our assistant to simulate an excitation RF pulse.
import json
# ask assistant to simulate an excitation pulse
thread, run = helper.create_thread_and_run(client, assistant, "Simulate an excitation pulse with pi/2 flip angle with 0 RF phase and initial magnetization of [0 0 1]")
run = helper.wait_on_run(client, run, thread)- Next, we extract the function name that the assistant is calling. For simplicity, we assume that the assistant has called the simrf() function, which it does. We blindly pass the arguments sent by the assistant to simrf().
- If you have multiple functions defined, the assistant can all any of those functions at any time with any arguments. This is important to understand. The assistant acts upon the natural language messages that you as an user send it. The assistant can independently decide how to react to those messages. For a complex system, with thousands of functions, the assistant may create function pathways that you as a human may not even have thought of! That’s where the power of AI comes in.
- In a later example when we simulate a full sequence we will cover how to parse the function names and call the correct functions in your library, without assuming the function that the AI might be calling.
# extract tool call
toolCall = run.required_action.submit_tool_outputs.tool_calls[0]
name = toolCall.function.name
args = json.loads(toolCall.function.arguments)
print("Called function name:", name)
print("Arguments:", args)
M = simrf(**args) # blindly pass the arguments sent by the assistant
print("M:", M)- Every time a function is called, we need to submit the function’s return value back to the assistant. This way the assistant ‘knows’ the results of its last action.
import numpy as np
run.status
run = client.beta.threads.runs.submit_tool_outputs(
thread_id=thread.id,
run_id=run.id,
tool_outputs=[
{
"tool_call_id":toolCall.id,
"output":json.dumps(M.tolist()),
}
]
)- Lastly, we will wait for run to complete and check the thread
run = helper.wait_on_run(client, run, thread)
helper.pretty_print(helper.get_response(client, thread))- Here’s the result. The assistant called the right function and obtained the resulting vector [0,1,0]. Moreover, the assistant explained the result. It informed us that the RF pulse rotated the longitudinal magnetization from the z-axis to the transverse xy-plane. That’s quite cool!
user: Simulate an excitation pulse with pi/2 flip angle with 0 RF phase and initial magnetization of [0 0 1]
assistant: The simulation of an excitation pulse with a π/2 flip angle and 0 RF phase on an initial magnetization of [0 0 1] results in a new magnetization vector of approximately [0, 1, 0]. The third component is a very small number close to zero which can be considered as zero due to numerical precision limitations in the computation. Therefore, the magnetization has been rotated from being aligned with the z-axis (along the main magnetic field) to lying fully in the xy-plane.
- Now we will simulate a spin echo sequence. Unlike the previous example, we will not assume what function the assistant called. We will parse the function names and call the matching procedure.
- For educational purposes, we make several simplifying assumptions: (a) The RF pulse is instantaneous, (b) flip angle is ideal, (c) there is a single spin, (d) the static field is homogeneous, (e) gradients are ignored for now. We will divide the sequence into three parts: a 90 degree RF pulse followed by a relaxation period of TE/2; a 180 degree refocusing pulse; followed by a relaxation period of TE/2. Consequently, we will make three separate message requests to our assistant.
run = helper.submit_message(client, assistant.id, thread, "Simulate a 90 degree RF pulse followed by a relaxation period of TE/2. Use T1 = 500 ms, T2 = 50 ms and TE = 10 ms.")
run = helper.wait_on_run(client, run, thread)
# extract tool calls
if run.required_action != None:
toolCalls = run.required_action.submit_tool_outputs.tool_calls
toolOutputs = []
M = None
for index, toolCall in enumerate(toolCalls):
print(index)
name = toolCall.function.name
args = json.loads(toolCall.function.arguments)
if index == 0:
M = args["M"]
print("Called function name:", name)
print("Arguments:", args)
print("M:", M)
if name == "simrf":
M = simrf(M, args["alpha"], args["phi"])
elif name == "simgr":
M = simgr(M, args["theta"])
elif name == "simrelax":
M = simrelax(args["M0"], M, args["T1"], args["T2"], args["t1t"], args["t2t"])
toolOutputs.append({"tool_call_id":toolCall.id, "output":json.dumps(M.tolist()),});
# need to submit all tool outputs together
run = client.beta.threads.runs.submit_tool_outputs(
thread_id=thread.id,
run_id=run.id,
tool_outputs=toolOutputs
)
run = helper.wait_on_run(client, run, thread)
helper.pretty_print(helper.get_response(client, thread))- And here’s the assistant’s response. The assistant called the right function, obtained the result and then went on to explain the effects of T1 and T2 relaxation.
user: Simulate a 90 degree RF pulse followed by a relaxation period of TE/2. Use T1 = 500 ms, T2 = 50 ms and TE = 10 ms.
assistant: After simulating a 90 degree RF pulse on an initial magnetization vector of [0 0 1], we obtain a rotated magnetization vector of approximately [0, 1, 0].
Then, following a relaxation period of TE/2 (which is 5 ms, as TE is 10 ms), considering T1 = 500 ms and T2 = 50 ms, the magnetization vector becomes approximately [0, 0.9048, 0.00995]. This indicates that the magnetization has started to relax back towards the equilibrium state with some recovery of the longitudinal magnetization and decay of the transverse magnetization due to T1 and T2 relaxation effects, respectively.
- Similarly, we make the other two requests. The tool call extraction and function calling code are not shown since they are same as above.
run = helper.submit_message(client, assistant.id, thread, "After the relaxation period simulate a 180 degree refocusing pulse.")
... # add tool call extraction and function call code
run = helper.submit_message(client, assistant.id, thread, "After the refocusing pulse, add another relaxation period of TE/2.")
... # add tool call extraction and function call code- Here’s the assistant’s response to our request to simulate a refocusing pulse. Again the assistant got the correct result and explained the physical effects of the phenomenon we are simulating.
user: After the relaxation period simulate a 180 degree refocusing pulse.
assistant: After the relaxation period, applying a 180 degree refocusing pulse to the magnetization vector [0, 0.9048, 0.00995] results in a new magnetization vector of approximately [0, -0.9048, -0.00995]. This refocusing pulse has inverted the sign of both the transverse and the longitudinal components of the magnetization.
- And here’s the response on our request to simulate a relaxation period of TE/2 after the refocusing pulse. Every time I run this, the assistant explains the result slightly differently, providing an unique insight. I find that quite intriguing.
user: After the refocusing pulse, add another relaxation period of TE/2.
assistant: After a refocusing pulse, adding another relaxation period of TE/2 (5 ms, as TE is still 10 ms) with T1 = 500 ms and T2 = 50 ms, the magnetization vector becomes approximately [0, -0.8187, 0.000099]. This reflects further relaxation effects with a continuing decrease in the magnitude of the transverse magnetization and a minimal change in the longitudinal magnetization, moving closer to equilibrium.
- We can visualize the simulation results by plotting the magnetization vector at different time points in the pulse sequence. The following plot includes the effects of a 15 Hz off-resonance which dephases the magnetization. But at TE, the spin echo sequence produces a nicely refocused signal. Remember, earlier in the post, we spoke about the spin echo sequence’s robustness to off-resonance effects!
- In addition to the parameters described above, we also simulated for a TR = 1 second. You can see how the longitudinal magnetization at time TR is less than 1 (0.86 to be precise). This indicates that the next acquisition has less initial magnetization available to generate a signal. Increasing the TR, would increase the amount of initial magnetization for the next repetition. But T1 recovery follows an exponential asymptotic function. So the longitudinal magnetization will never go to 1, no matter how large a TR you use. That’s in a way crazy!
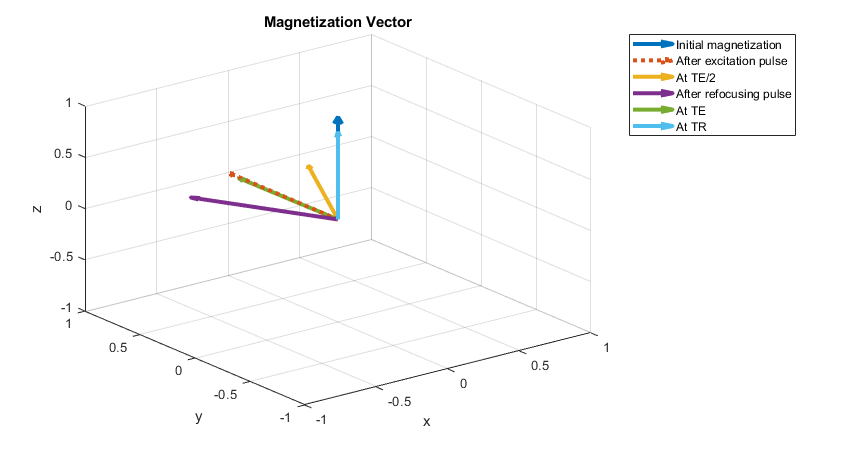
Knowledge Retrieval
So far we have explored the function calling capabilities of the OpenAI Assistants API. Now we will learn about the retrieval functionality. Retrieval allows developers to add information to the assistants knowledge base. This is quite powerful. Retrieval allows the GPT model to use knowledge beyond its training dataset.

- As an example, we will add Bloch’s Nuclear Induction paper to the assistant
file = client.files.create(
file=open(
"data/bloch_nuclearinduction.pdf",
"rb"
),
purpose="assistants",
)
assistant = client.beta.assistants.update(
assistant.id,
tools=[{"type":"retrieval"}],
file_ids=[file.id],
)- Let’s test if our assistant can answer questions related to Bloch’s paper. We will ask the assistant to explain the Bloch equations, listed as equation (38) in the paper.
run = helper.submit_message(client, assistant.id, thread, "Can you explain equation 38a, 38b and 38c from Felix Bloch's paper on nuclear induction.")
run = helper.wait_on_run(client, run, thread)
helper.pretty_print(helper.get_response(client, thread))- Here’s the assistant’s response
user: Can you explain equation 38a, 38b and 38c from Felix Bloch's paper on nuclear induction.
assistant: Equations 38a, 38b, and 38c from Felix Bloch's paper on nuclear induction are differential equations that describe the change in the components of the nuclear magnetization vector \(\vec{M}\) in response to an external magnetic field and internal relaxation mechanisms【35†source】.
Equation 38a:
\[ \frac{dM_x}{dT} = \gamma (M_y H_z - M_z H_y) + \frac{M_0 - M_x}{T_2} \]
This equation describes the rate of change of the x-component of magnetization \(M_x\). The first term on the right-hand side represents the precessional torque due to the cross product of the magnetization vector with the magnetic field vector, while the second term represents the relaxation of \(M_x\) towards its equilibrium value \(M_0\) over the transverse relaxation time \(T_2\).
Equation 38b:
\[ \frac{dM_y}{dT} = \gamma (M_z H_x - M_x H_z) \]
The y-component of magnetization \(M_y\) follows a similar precession mechanic due to the magnetic field, without an explicit relaxation term in this equation. As a side note, the inclusion of relaxation terms for \(M_y\) would be similar to the \(M_x\) counterpart, with a returning to equilibrium over time \(T_2\).
Equation 38c:
\[ \frac{dM_z}{dT} = \gamma (M_x H_y - M_y H_x) + \frac{M_0 - M_z}{
assistant: \frac{M_0 - M_z}{T_1} \]
The z-component of magnetization \(M_z\) also experiences a precessional term due to the magnetic field, in addition to a return to equilibrium represented by the second term, where the magnetization component relaxes or recovers towards its equilibrium value \(M_0\) over the longitudinal relaxation time \(T_1\).
That’s quite crazy! Do you think the assistant got it right? A human would need years of learning and training to comprehend these equations.
Summary
In this post we implemented an OpenAI assistant to simulate an MRI pulse sequence. We covered function calling and retrieval capabilities. The main goal of this post was to get you excited about LLMs and demonstrate how you can use it in your own work. For this, we used the example of an MRI spin echo sequence simulation with several simplifying assumptions. We did not cover OpenAI’s code interpreter functionality. It might be a good topic for a future post.
In the comments section, we would love to hear about your experience in building AI assistants.
Here are some key takeaways:
- An OpenAI assistant can be created with only a few lines of code
- Function calling allows the assistant to call procedures defined by you
- During function calling, the implementation details of your function are not exposed to the AI
- Through knowledge retrieval you can add data to the assistant beyond the model’s training dataset
Excellent post! We will be linking to this great post on our
website. Keep up the good writing.
My partner and I stumbled over here different web page and thought I might as well check things out.
I like what I see so now i am following you. Look forward to looking into your web page repeatedly.